面面垂直的判定方法

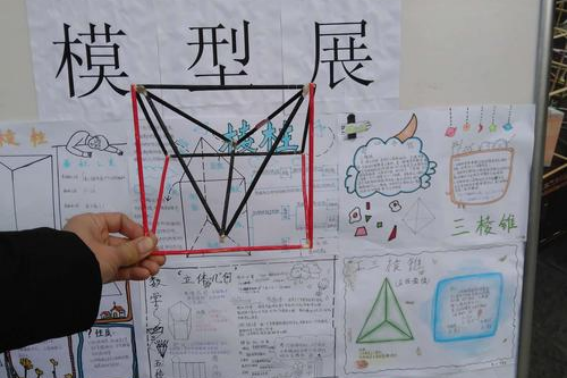
面面垂直的判定方法如下：

1、在一个平面内做2条相交直线，另一个平面内有一条直线垂直于这两条相交直线，则面面垂直。

2、如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面，则面面垂直。

3、如果一个平面经过另一平面的垂线，则这两个平面相互垂直。

面面垂直的证明方法：

1、利用直角三角形中两锐角互余证明。

由直角三角形的定义与三角形的内角和定理可知直角三角形的两个锐角和等于90°，即直角三角形的两个锐角互余。

2、勾股定理逆定理。

3、圆周角定理的推论。

直径所对的圆周角是直角，一个三角形的一边中线等于这边的一半，则这个三角形是直角三角形。

4、三垂线定理。

在平面内的一条直线，如果和穿过这个平面的一条斜线在这个平面内的射影垂直，那么它也和这条斜线垂直。

立体几何的平行关系与垂直关系的证明：

一、平行关系。

1、线线平行。

在同一平面内无公共点的两条直线平行；公理4（平行公理）；线面平行的性质。4.面面平行的性质；垂直于同一平面的两条直线平行。

2、线面平行。

直线与平面无公共点；平面外的一条直线与平面内的一条直线平行；两平面平行，一个平面内的任一直线与另一平面平行。

3、面面平行。

两个平面无公共点；一个平面内的两条相交直线分别与另一平面平行。

二、垂直关系。

1、线线垂直。

直线所成核则角为90°；一条直线与一个平面垂直，那么这条直差敏线与平面内的任一直线垂直。

2、线面垂直。

一条直线与一个平面内的任一直线垂直；一条直线与一个平面内的两条相交直线都垂直；面面垂直的性质；两条平行直线中的一条垂直与一个虚氏枝平面，那么另一直线也与此平面垂直；一条直线垂直与两个平行平面中的一个，那么这条直线也与另一平面垂直。

标签：判定,垂直