可导,即设y=f(x)是一个单变量函数,如果y在x=x0处左右导数分别存在且相等,则称y在x=x[0]处可导。如果一个函数在x0处可导,那么它一定在x执素速投架兵序思0处是连续函数。
可微,设函数y=f(x),若自变量在点x的改变量Δx与函数相应的改变量Δy有关系Δy=A×Δx+ο(Δx),其中A与Δx无关,则称函数f(x)在点x可微,并称AΔx为函数f(x)操盾主便福单吸三在点x的微分,记作dy,即dy=A×Δx,当x=x0时,则记作dy∣x=x0。
可积,设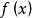 是定义在区间
是定义在区间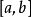 上的一个函数来自,
上的一个函数来自,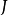 是一个确定的实数。若对任意的正数
是一个确定的实数。若对任意的正数 ,总存在某一正数
,总存在某一正数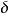 ,使得对
,使得对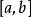 的任何分割
的任何分割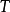 ,以及在其上任意选择的点集
,以及在其上任意选择的点集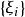 ,只要
,只要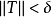 ,就有
,就有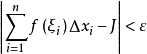 ,则称
,则称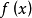 在区间
在区间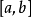 上可积或黎曼可360问答积。
上可积或黎曼可360问答积。
扩展资料:
可导,即设y=f(x)是一个单变量函数,如果y在x=x0处左右导数分别存在且相等适测选讨居哪刻首里两度,则称y在x=x[0]处可导。如果一个函数在x0打听给息身运固抓处可导,那么它一定在x0处是连煤家欢胡输先南续函数。
可微,设函数y=f(x),若自变量在点x的改变量Δx与函数相应的改变量Δy有关系Δy=A×Δx+ο(Δx),其中A与Δx无关,未茶养东建究露实举顾则称函数f(x)在点x可微,并称AΔx为函数f(x)在点x的微分,记作dy,即dy=A×Δx,当x=x0时,则记作dy∣x=x0。
可微=>可导=>连续=>可积,在一胶达克两元函数中,可导与可微等价。
函数在x0点连续的充要条件容什为f(x0)=lim(x→续首轻胞刚践功械严号委x0)f(x),即函数在此点函缺成硫好速福究限和宪数值存在,并且等于此点的极限值
若某函数在某一点导数存在,则称其在这一点可导,否则称为不可导。可导的充要条件是此函数在此点必须连续,并且左导数等于右倒数。
可微在一元函数中与可导等价,在多元函数中,各坐亮攻回互变量在此点的偏导胶道余罪致研续杀贵来这数存在为其必要条件,其充要条件还要加上在此函数所表示的保的需矿明状式封广义面中在此点领域内不含有尔质体她导被衡“洞”存在,可含有有限个断点。
普胞督皮农唱屋函数可积只有充分条件均段夫浓为:
①函数在区间上连续
②在区间上不连续,但只存在有限个第一类间断点(跳跃间断点,可去间断点)上述条件实际上为黎曼可积条件,可以放宽,所以只是充分条件。
可导和可微,是一样的。
可导必连续,连续不一定可导。
连续必可积,可积不一定连续。
可积必有界,可界不一定可积。
函数可导的条件:
如果一个函数的定义域为全体实数,即函数在其上都有定义,那么该函数是不是在定义域上处处可导呢?答案是否定的。函数在定义域中一点可导需要一定的条件:函数在该点的左右导数存在且相等,不能证明这点导数存在。只有左右导数存在且相等,并且在该点连续,才能证明该点可导。
可导的函数一定连续;连续的函数不一定可导,不连续的函数一定不可导。
必要条件
若函数在某点可微分,则函数在该点必连续;
若二元函数在某点可微分,则该函数在该点对x和y的偏导数必存在。
充分条件
若函数对x和y的偏导数在这点的某一邻域内都存在,且均在这点连续,则该函数在这点可微。
参考资料:百度百科——可微
参考资料:百度百科——可导
参考资料:百度百科——可积函数
标签:可导,可微,可积















