增长率问题探索
增长率问题是近几年中考的热点题型,只有掌握增长誉山率问题的本质内涵,才能在中考时以不变应万变。
增长率实质是;增加量占起始量的百分比庆渗中,增加量是终极量减去
起始量。
设起始量为q,终极量为p ,增长率为x 则增长一次为p=q(1+x) l连续增长二次为p=q(1+x)2
.若x>0,表示增长;若x<0,表示降低.
一、 平均增长率
例1: 某果园今年栽种果树200棵,现计划扩大栽种面积,使今后两年的栽种量都比前一年增长一个相同的百分数,这样三年(包括今年)的总栽种量为1400棵,求这个百分数
分析:设增长率为x则明年栽种量为200(1+x),后年栽种量为200(1+x)2
则三年总栽种量为200+200(1+x)+200(1+x)2
解:设增长率为x则根据题意得
200+200(1+x)+200(1+x)2=1400
设1+x=y则200+200y+200y2=1400
解之得 y1=2 y2=-3
即1+x=2或1+x=-3
X1=1 x2=-4
所以这个百分数为100%
例2:某商厦二月份的销售额为100万元,三月份销售额下降了20%。商厦从四月份起改进经营措施,销售额稳步上升,五月份销售额达到135.2万元,试求四、五两个月的平均增长率.
分析:先算出三月份的销售额为100(1-20%)万元.设四、五两个月的平均增长率为x,则四月份销售额为100(1-20%)(1+x)万元,五月份的销售额为100(1-20%)(1+)(1+)=100(1-20%)(1+x)2万元,于是可列出方程100(1-20%)(1+x)2=135.2.
解:设四、五两个月的平均增长率为,由题意得方程
100(1-20%)(1+x)2=喊没135.2
(1+x)2=1.69
即1+x=±1.3
故x1=0.3,x2=-2.3
因为x2=-2.3不符实际,舍去,所以x=0.3=30%,
即四、五两个月的平均增长率为.
专项练习:
1、某县为发展教育事业,加强了对教育经费的投入,2007年投入3 000万元,预计2009年投入5 000万元.设教育经费的年平均增长率为,根据题意,下面所列方程正确的是( )
A.3000(1+x)2=5000 B.3000x2=5000
C.3000(1+x%)2=5000 D.3000(1+x)+3000(1+x)2=5000
2、某电动自行车厂三月份的产量为1000辆,由于市场需求量不断增大,五月份的产量提高到1210辆,则该厂四、五月份的月平均增长率为________.
3、某商品经过两次连续降价,每件售价由原来的55元降到了35元.设平均每次降价的百分率为x,则下列方程中正确的是( )
A.55 (1+x)2=35 B.35(1+x)2=55 C.55 (1-x)2=35 D.35(1-x)2=55
4、某种商品零售价经过两次降价后的价格为降价前的,
则平均每次降价( )
A.10% B.19% C.9.5% D.20%
二、变化的增长率
例3 :K国某种商品今年2月份的进口量比上年末减少了20%,由于该种商品价格上涨,进口该种商品的费用反而比上年末 增加了30%,2月份的涨幅比1月份的涨幅多5%,求1月份该种商品价格相对上年末的增长率。
分析: 设上年末该种商品的进口量为a,该种商品价格为b,今年1月份的价格增长率为x,则今年2月份该种商品的进口量为(1-20%)a,1月份的价格为b(1+x) 2月份价格为b(1+x)(1+x+5%),今年2月份的费用为(1-20%)a×b(1+x)(1+x+5%)
解:今年1月份的价格增长率为x 则根据题意得
(1-20%)a×b(1+x)(1+x+5%)=ab(1+30%)
化简整理 得8(1+x)2+0.4(1+x)-13=0
令 1+x=y则 8y2+0.4y-13=0
解之得 y1=1.25 y2=-1.3
即 1+x=1.25 或 1+x=-2.3
∴ x1=0.25=25% x2=-2.3(舍去)
所以1月份该种商品价格相对上年末的增长率为25%
点评:本题是一个变化的增长率问题.如果设增长前的值为a, 第一次增长率为x, 第二次增长率比第一次增长率多m, 那么第二次增长率为(x+m),增长后的结果为b,由题意列出方程的方法可以概括为公式a (1+x)(1+x+m)=b.当m =0时,变化的增长率问题就成为平均增长率问题
专项练习:1(陕西省中考题)有一商场在第一季度内将某种家电商品连续降价,其中3月份的降幅比2月份的降幅要多2个百分点(一个百分点=1%),结果3月份的销售台数比1月份增加4倍,销售收入增加296%.问2月份在1月份的基础上降价百分之几?
三、相关的增长率
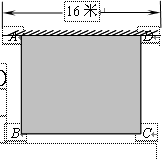
例3、如图所示,某幼儿园有一道长为16米的墙,计划用32米长的围栏靠墙围成一个面积为120平方米的矩形草坪ABCD.求 1. 矩形草坪BC边的长.
2.在第1问的条件下,若去掉墙长为16米的限制条件,扩大矩形草坪ABCD的面积为216平方米,其中BC的增长率是AB增长率的2.5倍,求AB边的增长率。
解:1. 设AB的长为x 米则BC边的长为(32-2x)米 根据题意得
X(32-2x)=120
解之得:x1=10 x2=6
当x=10时AB为10米,BC为12米
当x=6时AB为6米,BC为20米>16米,不合题意根据题意得
所以矩形草坪BC边的长为12米.
2.设AB边的增长率为y则BC边的增长率为2.5y,
根据题意得 10(1+y)×12(1+2.5y)=216
解之得 y1=0.2=20% y2=-1.6(舍去)
所以AB边的增长率为20%
专项练习:
1(南京市中考题)某农场种植了10亩地的南瓜,亩产量为2000kg,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜的种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60000,求南瓜亩产量的增长率.
标签:增长率,数学