欧拉公式

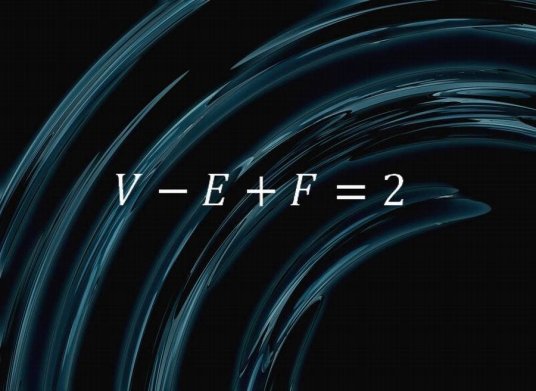
复变函数中，e^(ix)=(cos x+isin x)称为欧拉公式，e是自然对数的底，i是虚数单位。

拓扑学中，在任何一个规则球面地图上，用 R记区域个 数 ，V记顶点个数 ，E记边界个数 ，则 R+ V- E= 2，这就是欧拉定理 ，它于 1640年由 Descartes首先给出证明 ，后来 Euler(欧拉 )于 1752年又独立地给出证明 ，我们称其为欧拉定理 ，在国外也有人称其 为 Descartes定理。

想要了解更多欧拉公式, 欧拉公式复变函数, 欧拉公式欧拉公式证明, 欧拉公式拓扑学, 欧拉公式拓扑学证明, 欧拉公式分式, 欧拉公式平面几何, 欧拉公式统计学, 欧拉公式物理学, 欧拉公式图论的信息，请点击：欧拉公式百科

标签：欧拉公式,欧拉,公式,拓扑学