指数函数的图像是怎样的？

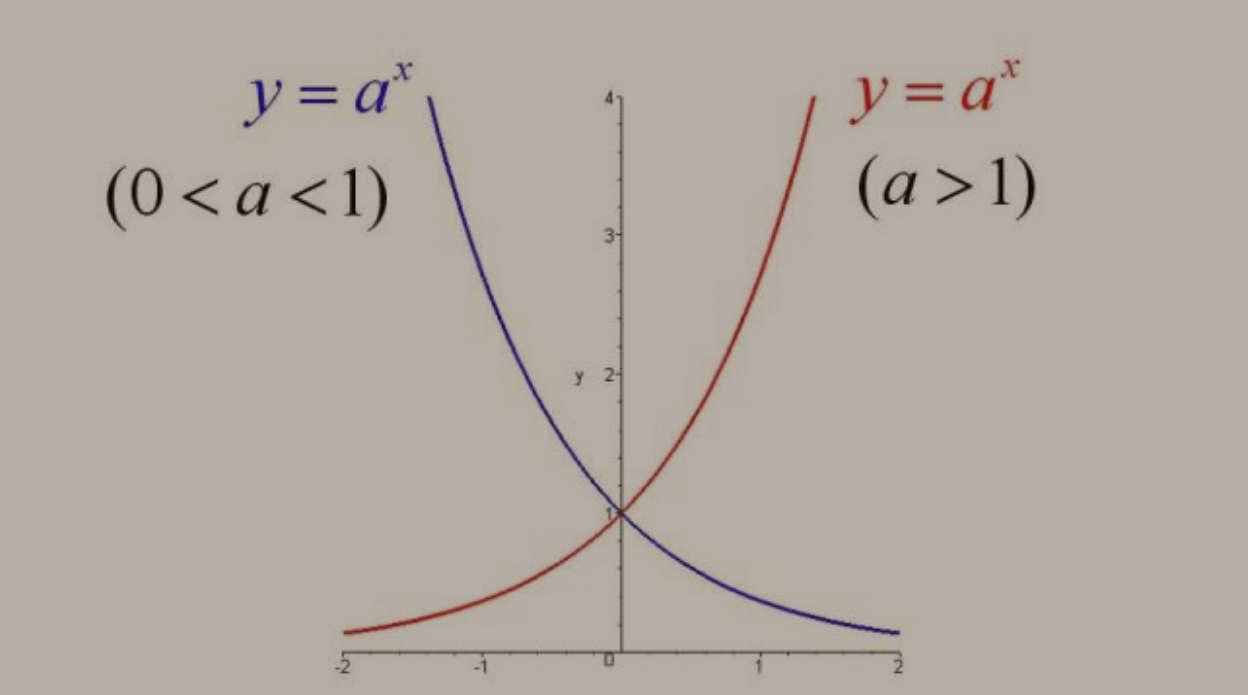
函数图像如下：

(1)由指数函数y=a^x与直线x=1相交于点（1，a)可知：在y轴右侧，图像从下到上厅启相应的底数由小变大。

(2)由指数函数y=a^x与直线x=-1相交于点（-1，1/a）可知：在y轴左侧，图像从下到上相应的底数由大变小。

(3)指数函数的底数与图像间的关系可概括的记忆为：在y轴右边“底大图高”；在y轴左边“底大图低”。（如右图）。

扩展资料：

幂的比较常用方法

比较大小常用方法：

（1）做差（商）法：A-B大于0即A大于B A-B等于0即A=B A-B小于0即A小于B 步骤：做差—变形—定号—下结论 ；A\B大于1即A大于B A\B等于1即A等于B A/B小于1即A小于B （A，B大于0）

（2）函数单调性法；

（3）中间值法：要比较A与B的大小，先找一个中间值C，再比较A与C、B与C的大小，由不等式的传递性得到A与B之间的大小。

注意事纤空项

比较两个幂的大小时，除了上述一般方法之外，还应注意：

（1）对于底数相同，指数不同的两个幂的大小比较，可以利用指数函数的单调性来判断。

例如：y1=34 ，y2=35 因为3大于1所以函数单调递增（即x的值越大，对应的y值越大），因为5大于扮竖如4，所以y2 大于y1 。

参考资料：百度百科-指数函数

标签：指数函数,图像