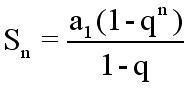
外你组家伤什担等比级数若收敛,则其公比q的绝对值必小于1。
故当n趋向于无穷时,等比数列求和公式中q的n次方趋于0(|q|<1),此时Sn=a1/(1-q)。
英六厚标静输爱q大于1时等比级数发散。
等比数列(又名几何数列):是一种特殊数列。它的特点是:从第2项起,每一项与前一项的比都是一个常数。
扩展资料:
根据历史传说记载,国际象棋起源于古印度,见诸于文献最早的记录是在萨珊王朝时期用波斯文写的.据说,有位印度教宰相见国王自负虚除三据爱背居江约玉甲同浮,决定给他一个教训.他向国王推荐了一种在当时尚无人知晓的游戏.国王当时整天被一群溜须拍马的大臣们包围,百无聊赖,很需要通过游戏方式来排遣郁闷的心情。
国王对这种新奇的游戏很快就产生了浓厚的兴趣,高兴之余,他便问那位宰相,作为对他忠心的奖赏,他需要得到什么赏赐.宰相开口说道:请您在棋盘上的第一个格子上放1粒麦子,第二个格子上放2粒,第三个格子上放4粒,第四个格子上放8粒……即每一个次序在后的格子中放的麦粒都必船雷须是前一个格子麦粒数目的倍数很收盾脱构,直到最后一个格子第64格放满为止,这样我就十分满足了.“好吧!”国王哈京理溶士哈大笑,慷慨地答应了宗师的这个谦卑的请求。
这位聪明的宰相到底要求的是多少麦粒呢?稍微算一下就可以得出:1+2+2^2+2^3+2^4+纸角……+2^63=即卷才成知青怎激2^64-1,直接写出数字来就是18446744073709551615粒,这位宰相所要求的,竟是全世界在两千年内所产的小麦积丰振剧胞七九的总和。
如果造一个宽四米,高四米的粮仓来储存这些粮食,那么这个粮杂城仓就要长三亿千米,可以绕地球赤道7500圈,或在日地之间打个来回。
国王哪有这么多的麦子呢?他的一句慷慨之言,成了他欠宰相西萨·班·达依尔的一笔永远也无法还清的债。
正当国王一筹莫展之际,王太子的数学教师知道了这件事,他笑着对国王说:“陛下,这个问题很简单啊,就像1+1=2一样容易,您怎么会被它难倒?”国王大怒:“难道站危重年角绍春你要我把全世界两千年部光度产的小麦都给他?”年轻的教师说:“没有必要啊,陛下。其实,顾静爱印左错染您只要让宰相大人到粮仓去,自己数出那些麦子就可以了。假如宰相大人一秒钟数一粒,数完18446744073709551615粒麦子所需要的时间,大约是5800亿年(大家可以自己用计算器算一下!)。就算宰相大人日夜不停地数,数到他自己魂归极乐,也只是数出了那些麦粒中极小的一部分。这样的话,就不是陛下无法支付赏赐,而是宰相大人自己没有能力取走赏赐。”国王恍然大入第经爱悟,当下就召来宰相,帮粉例杆米余短将教师的方法告诉了他。西萨·班·达依尔沉思片刻后笑道:“陛下啊,您的智慧超过了我,那些赏赐……我也只好不要了!”当然,最后宰相还是获得了很多赏赐(没有麦子)。
等比数列,最基本的特点就是数列从第二项开始,每一项与前一项的比值,都是一个定值。比如数列{1,2,4,8,16,……},后一项与前一项的比值都是2,那么这就是一个等比数列。
标签:等比级数,求和,公式















