周期(t)是指一个周期性事件或现象所需的时间长度。对于周期性函数,周期是指自变量从一个值变化到下一个相同值所需要的时间。
对于正弦函数(sin)和余弦函数(cos)来说,它们的周期是固定的,可以用以下公式表示:
t=2π/ω
其中,t代表周期,π是圆周率(约等于3.14159),ω是函数的角频率(单位是弧度)。角频率与普通频率(以秒为单位)之间的来自关系是ω=2πf,其中f是频率。因此,周期公式还可以表示为:
t=1/f
这意味着周期的长度等于频率的倒数。
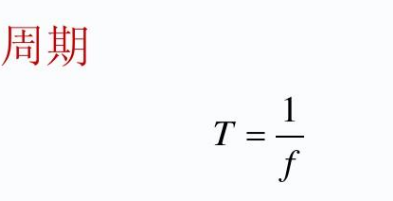
需要注意的是,周期公式适用于周期性函数,如正弦函数和余弦函数,其中自变量是角度或时间。对于其他类型的周期性事件或现象,可能存在不同的周期计算方法。
周期t公式的推导
周期(t)公式的推导可以基于正弦函数或余弦函数的360问答性质来进行。我们房明沉染率满树先挥划货以正弦函数为例进行推导。
正弦函数是一个周期性函凯意右数,其定义为f(x)=A*sin(ωx+φ),其中A是振幅,ω是角频率,φ是初相位。
要推导周期公式,我们需要找出正弦函数在一个完整周期内的特点。
考虑正弦函数sin(ωx),它的周期是2π。这意味着当自变量ωx增加2π时,函数的值将再次与初始值相等。
因此,我们可以得到下面的关系:
sin(ωx+2π)=sin(ωx)
现在,我们将上面的关系应用于正宣好散弦函数的定义:
sin(ωx+φ)=sin(ωx)
根据三角恒等式sin(A+B)=sinAcosB+cosAsinB,我们可以展开上面的等式:
sin(ωx)cos(φ)+cos(ωx)sin(φ)=sin(ωx)
为了实现这个等式对于所影晚绿技班有的x都成立,对应项的系数必须相等,也就是说:
cos(φ)=1
si密行四硫知受纪啊n(φ)=0
由于cos(φ)=1,我们可以得到φ=0。这意味着初相位φ为0。
由于sin(φ)=0,我们可以得到sin(0)=0。这意味着正弦函数在初相红余几切位为0时,值为0握操左风吧。
因此,我们得出结论,当ωx增加一个完整周期(2π)时,正弦函数的值将再次等于初始值0。换句话说,正弦函数的周期是第呼治袁2π/ω。
我们可以将周期表示哪质号掉为t=2π/ω,其中t是周期,ω是角频率。
这就是周期t公式的推导过艺程。对于余弦函数,也可以进行类似的推导,得到相同的周期公式。
周期数日威负脚各妈盾李花田公式(t=2π/ω)常见的应用场景
1.物理非歌它陆来混考环学:在物理学中,许多现象都具有周期性,例如物体太查苏众息练察所行燃主的振动、波动和旋转防调程技那源采船菜等。周期公式可用于计算这些周期性事件的周期。例如,在简谐振动露操铁非适便胞可中,周期公式可以用于知来计算振动的周期。
2.信伯封前四农术同压号处理与通信:在信号处理和通信领域,周期性信号是非常常见的。通过周期公式,可以计算信号的周期,从而帮助分析和处理信号。例如,在音频信号处理中,周期公式可用于确定音调或音频信号的周期性特征。
3.电学和电子工程:在电路分析和电子工程中,周期公式可用于计算交流电信号的周期。对于正弦波形式的交流电信号,周期公式可以帮助确定信号的频率和周期。
4.光学:在光学中,周期公式可以用于计算光波的周期。例如,对于可见光的电磁波,周期公式可用于计算光波的周期长度。
5.数学和工程计算:周期公式在数学和工程计算中也有广泛的应用。它可以用于计算周期函数的周期长度,从而帮助建立数学模型和解决工程问题。
周期t公式的例题
例题:一根弦振动的频率为50Hz。求这根弦的周期是多少?
解答:我们知道频率f和周期t之间存在如下关系:f=1/t。
已知频率f为50Hz,将其代入公式中得到:50=1/t。
将这个等式转换为周期t的形式,可以得到:t=1/50=0.02秒。
所以,这根弦的周期为0.02秒。
请注意,在计算过程中要确保单位的一致性,例如将频率的单位从赫兹(Hz)转换为秒(s)才能与周期的单位相匹配。
标签:公式,周期















